Where Theory Meets Practice Archives
Where Theory Meets Practice: Transformations and Reference Frames, Part 2
In the previous article (PSM Dec. 2013), I mention the practical problems of control being in different reference frames, and I present the surveying solution to this problem. In this article I address how to determine if the localization process was successful. To do this we will need to look at the statistics of the […]
Where Theory Meets Practice: Geodetic Observations: Part 1
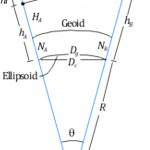
Since the inception of GPS in the 1980s, surveyors have been presented with GPS baseline reduction results that list both geodetic azimuths and distances for the baseline vectors. In Part I of this article, I present the difference between the normal to the geoid and ellipsoid, which is known as deflection of the vertical, and […]
Where Theory Meets Practice: Geodetic Observations – Part 2
Part 1 of this article (March 2014) presents the differences between azimuths that surveyors observe with a total station and the geodetic azimuths listed in GNSS adjustment reports. However, the effect on angles caused by the deflection of the vertical at the observing station is typically small. Thus, the difference between the observed astronomic angle and […]
Geodetic Observations, Part 3
Types of Distances for Geodetic Observations This article explores the various types of distances that are often listed on GNSS adjustment reports; for related articles on the difference between geodetic and observed azimuths and angles, see “Where Theory Meets Practice” in Professional Surveyor’s March and May 2014, issues. Slope (slant) distances (S) observed on the […]
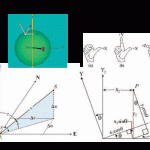
Transformation of Observations
Educate: Where Theory Meets Practice In previous articles I’ve discussed the reduction of conventional surveying observations to their geodetic equivalents. This article presents how these observations can be reduced to simple vector components that match GNSS surveyed baseline vectors. Unfortunately this transformation of conventional observations to GNSS baseline vectors involves three-dimensional rotations, so the mathematics will increase. […]
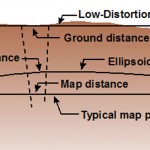
Transformation of Observations Part 2
In my previous article in the September issue, I demonstrate one method of taking conventional/optical observations and converting them into GNSS baseline vectors. Here I demonstrate how to create a map projection system that is near the ground, and thus on the surface we survey. These map projections are commonly referred to as low-distortion projections; […]