In the 1930s when the National Geodetic Survey (NGS), formerly the Coast and Geodetic Survey, created the first state plane coordinate system (SPCS), they limited the precision between a geodetic (ellipsoid) distance and the map distance to a precision of 1:10,000 or better by limiting the width of the zones. This resulted in many states with multiple zones.
These coordinate systems served the nation’s surveyors well until recent times when the precision of the instruments allowed surveyors to easily achieve precisions greater than 1:10,000. Additionally, these multiple zones have complicated surveys when they are crossed and the lives of people working in geographic information systems (GIS) because this implies multiple zone conversions for many states.
However, in the NGS’s ten-year plan, a new national reference system to support work using global navigation satellites systems (GNSS) will be created. This new system, along with a gravity-based geoid, will ease the differences between GNSS surveys and our national datum. When this happens, NAD83 and its many variants will be finally put to rest. Hopefully near this time, the NGS will also revisit the state plane coordinate system designed for each state.
Judging by the number of phone calls and emails I receive about the misclosure of a link traverse using state plane coordinates, it is apparent that many surveyors either do not understand the need for the reduction of observed horizontal distances to their equivalent map projection lengths or simply do not wish to perform these reductions. Because surveyors are not willing to work in a geodetic coordinate system and the developable surface of a map projection cannot fit the surface of the Earth perfectly, failure to reduce horizontal distances to the map projection surface will always result in error, which will be shown in the relative precision and misclosure of a link traverse.
Additionally, all surveyors will tell you that they work on the surface of the Earth and not on the map projection’s developable surface. If layout distances from a state plane coordinate system are not brought up to the surface of the Earth, the object being laid out will be incorrect. However, these differences in distances can be avoided if the developable surface of the map projection is made coincident with the topographic surface of the Earth.
Local Map Projection Systems
Some areas of the country have pursued this goal by developing local map projection systems that fit the average elevations for a region. For example, Wisconsin has developed individual map projection systems for every county to nearly fit the developable surface of the map projection to the topographic surface. It is my understanding that other locations in the high plains of the west have approached this problem similarly.
However, what this has created is a multitude of map projection zones that must be dealt with correctly each time a survey crosses into another zone. It is my opinion that this is not the best solution to the problem. In fact, the reason for this series of articles is to inform surveyors of the correct procedures to use when working with a map projection system, which will help maintain their survey precisions regardless of the map projection employed.
Still, areas such as the western high plains do have a unique problem. For example, Denver, Colorado is known as the mile-high city. At 5280 ft, the elevation factor results in a precision between a map projection distance and a distance observed on the topographic surface of only 1:4000. At 7100 ft, Flagstaff, Arizona surveyors are dealing with an elevation factor that renders distance precision less than 1:3000. Obviously, in these areas it is imperative to properly reduce observed distances or bring map distances back up to the surface if the current state plane coordinate systems are to be used.
Here is our opportunity. Since the NGS has already stated that it will change to a new reference frame (datum) in the upcoming years, this provides surveyors with a chance to eliminate some of the problems caused by the elevation of the topographic surface. To understand how this problem can be reduced, we need to understand how map projections are developed.
How Map Projections Are Developed
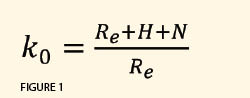For example, the defining parameters for the transverse Mercator map projection are latitude and longitude (φ0, λ0) of the map projection’s origin, scale factor k0 for the central meridian of the zone, and false easting E0 and false northing Nb, which are used to prevent negative coordinates in the zone and areas immediately surrounding it. In SPCS 27 and SPCS 83, the scale factor at the central meridian was limited to 0.9999, which provided a 1:10,000 or better distance precision between a map distance and its equivalent geodetic distance. It did not consider the distances we measure on the surface of the Earth where the elevation factor can easily produce distance precisions that are less than 1:10,000 for locations above approximately 2200 ft. 
If we are to bring the developable surface of this map projection to the topographic surface of the Earth, we need to select a scale factor that raises the developable surface up to the average topographic surface of the Earth. The defining parameter for the scale factor at the central meridian of a transverse Mercator zone can be computed as seen in Figure 1, where k0 is the scale factor for the transverse Mercator projection at the central meridian, Re the average radius of the Earth (which is approximately 6,371,000 m), H the average orthometric height of the map projection, and N the average geoid height for the map projection.
As an example, the average elevation of Arizona is 4100 ft, which is about 1250 m. The geoid height is about −26 m. Thus, a central meridian scale factor for a new transverse Mercator zone with the developable surface at 4100 ft would be approximately 1.00019212 (see Figure 2).
An observed horizontal distance is “reduced” to the map projection surface using the product of the elevation factor and the scale factor for the line, which is known as the combined factor. By selecting a defining scale factor that is the reciprocal of the elevation factor, it brings in the developable surface of the map projection to the average elevation of the region. If everything else remains the same for the Arizona SPCS 83 central zone, the scale factor for a line in Flagstaff would be about 1.00020040. Since the city is at an elevation of 2130 m approximately, the elevation factor for Flagstaff would be about 0.99966986 (see Figure 3).
The combined factor for a distance in Flagstaff would be approximately 0.99987020 (see Figure 4).
This combined factor would yield a distance precision between the surface distance and the map distance of 1:7700, which is still less than 1:10,000 but much closer than the 1:2000 that surveyors experience with the current SPCS system. This precision is similar to what surveyors on the east coast may experience when they survey a site above an elevation of 700 ft having a scale factor of 0.9999. While this precision is still low, it is much better than the existing system.
For Higher Precision
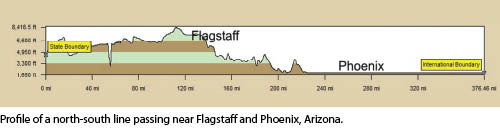If a higher precision is desired between the ground distance and the map distance, then additional information is needed. For example, shown in Figure 5 is the profile of a north-south line that runs near Phoenix and Flagstaff. Notice that the two major population centers are at extremely different elevations, where Flagstaff is at approximately 7100 ft and the Phoenix area is at 1100 ft. In the past, the transverse Mercator map projection was used for states like Arizona because its scale does not change along a north-south line, which matches the longest dimension of the state.
However, it is apparent from Figure 5 that one zone covering both the southern and northern portions of the state must fit two locations at very different elevations. Thus, another approach would be to divide the three zones in this state into six different transverse Mercator zones where three would be designed for elevations common in the southern part of the state and the other three for the northern part of the state. In the case of the central zone, the scale factor of 1.00033025 for the central meridian in the northern portion could be chosen for the elevation of Flagstaff, and the scale factor of 1.00004928 for the southern zone could be chosen for the Phoenix area.
This would mean that the computed scale factor for Flagstaff would be about 1.00034, and, when multiplied by its elevation factor of 0.999674, a combined factor of 1.00001 would result. This results in distance precision between the surveyed horizontal distance and the map projection distance of about 1:72,000. However, the result would be six state plane coordinate system zones where ground distances would closely match their map distances with a precision much better than 1:10,000. It would also be possible to divide the state into two zones where one would cover the northern portion and the other the southern portion. However, surveyors in transverse Mercator states would then have to become comfortable with convergence angles that are typical in states using the Lambert Conformal Conic map projection.
The disadvantage of adding zones, of course, would be that any time a survey crosses a zone, the difference in the two coordinate systems must be reconciled.1 By adding more zones to the state, crossing zones would occur more frequently. Additionally, having several different zones in a state is not convenient for the generation of statewide GISs where different coordinate systems must be reconciled. In fact, many in the GIS community would like to see a single coordinate system for an entire state.
The NGS has stated that it will introduce a new datum in 20222. Some have also stated that the need for a map projection system like the state plane coordinate system is unnecessary because GNSS will be able to bring national datum coordinates to most locations within minutes and because software can easily handle the rigorous geodetic computations. If this is the case then traditional map projection coordinate systems will be a thing of the past as everyone performs their daily business with geodetic coordinates. Unfortunately, I do not think that this train of thought matches reality because surveyors and construction companies who are unfamiliar with map projections are even more unfamiliar with computations on the ellipsoid.
Help Decide
The NGS is looking for your input on this matter. Will you feel comfortable working in a geodetic coordinate system, or is a map projection system like the state plane coordinate system–that allows you to achieve geodetic accuracies with plane computations–more to your liking? If the latter is the case, you need to tell Joe Evjen at Joe.Evjen@noaa.gov or your closest state geodetic advisor. If a map projection is your choice, now is the time to start thinking about what your next state plane coordinate system should look like. Decisions involving all constituents in the geospatial industries need to be considered, and the most agreeable solution for all adopted. In this case, the profession of surveying needs to consider the needs of the entire geospatial community.
The decision to use 1:10,000 precision for map projection accuracies was based upon the available technology in the 1930s. Although the science has not changed, the technology has moved the science closer to reality. We therefore need to revisit these decisions with the knowledge of the science and technology in the future. Now is the time for state societies to decide what their future will be.
Endnotes:
- Ghilani, C. 2013. “SPCS Zone Conversions.” Professional Surveyor Magazine, 33 (No. 5):2–5.
- Minkel, D.H. and M.L. Dennis. (2012), “Frames for the Future — New Datum Definitions for Modernization of the U.S. National Spatial Reference Systems: Replacing NAD 83 (Part 4 of 4).” The American Surveyor, 9 (No. 4): 22–33.
SIDEBAR
Formal Education
I wish to stand on my soap box for a moment. There is an alternative solution to the problem of using map projections, and that is a formal education. This problem of working with state plane coordinate systems at any elevation is an educational problem. Map projection systems provide 1-to-1 relationships between points on the surface of the Earth and the map projection when the observations are handled properly.
Often I hear surveyors talk about the fact that we are the experts in measurement. This statement involves more than simply pushing a button on an expensive piece of precise equipment. In fact, if that is all it involves, we will be replaced by technology in the near future. Being an expert also involves knowing how to handle measurements once they are observed. Too many of today’s surveyors are legal experts at determining boundary locations but not at handling the measurements they collect. There is too much reliance on software solutions to measurement problems.
Simply stated, if the distances are properly reduced, any map projection system will allow the surveyor to achieve geodetic computational accuracies with plane computations. Too many surveyors in too many states, including my own, believe they can learn everything they need to practice surveying through practice and self-education. However, the days of self-education left with the improvements in instrumentation during the 1970s. At that time, the abilities of our instrumentation started to uncover data-handling problems that demonstrated the lack of understanding in the profession. It is time for state societies to determine whether our industry wishes to be considered professionals or technicians. This decision has already been made by others in a few states. The difference between a professional and a technician is simply a formal education. Experience is extremely important but so is formal education.
