Using a Project Factor
In Part 1 of this series of articles (September 2014 issue), I explained how to transform surface observations into a geocentric coordinate system so that it could be compared to GNSS baseline vectors. In Part 2 (December 2014) I explained how the creation of a low-distortion map projection will bring the mapping surface up to the ground and thus provide a close comparison between GNSS and optical observations. In this article I discuss some of the disadvantages in using a low-distortion projection, and I introduce an alternate method that can be easily implemented in the field with survey controllers that are already available.
Disadvantages of a Low-distortion Map Projection
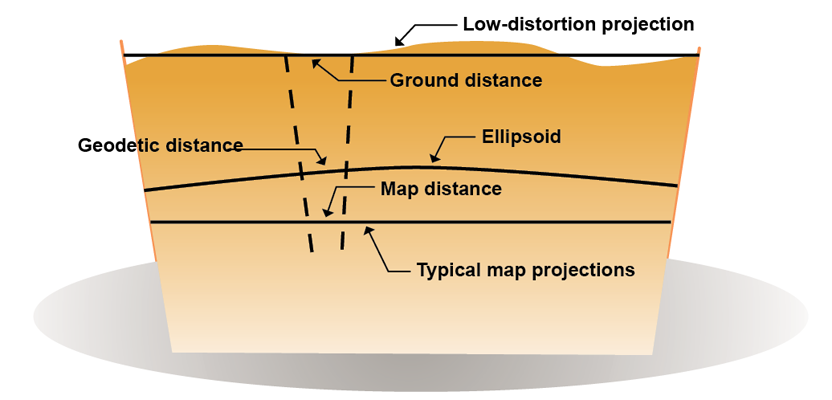
While low-distortion map projections have several obvious advantages, they also introduce disadvantages that should be considered. Realize that every time a low-distortion projection is created, you are creating a different coordinate system that can only be related to others through their geodetic coordinates. Thus, every time a low-distortion projection is created, it is a requirement to document and maintain the defining parameters for the low-distortion projection in perpetuity.
This is a major difference between using state plane coordinates and a low-distortion map projection. In the case of the state plane coordinate system, the defining parameters are maintained by the National Geodetic Survey (NGS) and are available in your software. On the other hand, each time you try to transform coordinates from a low-distortion projection, the software must “know” the defining parameters in order to perform this transformation.While low-distortion map projections have several obvious advantages, they also introduce disadvantages that should be considered. Realize that every time a low-distortion projection is created, you are creating a different coordinate system that can only be related to others through their geodetic coordinates. Thus, every time a low-distortion projection is created, it is a requirement to document and maintain the defining parameters for the low-distortion projection in perpetuity.
For example, assume that a low-distortion map projection for Luzerne County, Pennsylvania, is created by a company to simplify the work on a large-scale, countywide project (as was discussed in the previous article). Years later, the company is contracted to perform another job in the county. The first problem would be to find the defining parameters used to create the control station coordinates for the initial job. If the defining parameters for the low-distortion map projection were not documented or could not be located, the control coordinates created in the initial project could not be related to the current job or the National Spatial Reference System without first performing a localization.
In essence, this would be no different than initially using an arbitrary coordinate system. Assume that your client also needs state plane coordinates for the stations created in the survey. Again, if the defining parameters are not maintained, a localization of the stations into a defined geodetic coordinate system would be required to convert the low-distortion map projection coordinates into their equivalent geodetic coordinates. This would be no different than having arbitrary coordinates.
Thus, it is essential when creating a low-distortion projection to document and maintain the defining parameters in perpetuity. Failure to do so will remove some of the key advantages of a low-distortion map projection over an arbitrary coordinate system. Additionally, all field crews working on the project must have the same defining parameters in their survey controllers, or significant
errors can occur.
Additionally, as was demonstrated in the last article, variation in elevation can play a significant role in the quality of the low-distortion projection. This effect can be minimized by covering a smaller region, which would improve the distance precision in the projection. But, this solution then results in the possibility of needing more than one low-distortion projection to cover current or subsequent work in the area. In essence, you will introduce the problem of needing to cross zones. (The process of crossing zones was discussed in the May, 2013 issue of Professional Surveyor.) Again this leads to a less-than-ideal solution to the problem where elevation variation is significant.
There is still a difference between geodetic and grid azimuths. Thus, convergence angles are required to correct for the convergence of the meridians in order to compute a traverse in the low-distortion projection properly. In the projection created for Luzerne County in the previous article, this difference ranged from 0° to 15′. Thus, whenever a geodetic azimuth is used in computations, the convergence angle for the particular location must be computed and applied to obtain its equivalent grid azimuth. This requirement is no different than that required when using state plane coordinates.
Determining the “best” defining parameters for a region is not always quick, either. In order to check the precision of the projection, geodetic computations of the end points of lines at varying elevations are needed. Most surveying offices will not have this type of software available. However, the National Geodetic Survey does have this software in their geodetic
toolkit.
Because of this test, it was noted that several iterations of various k0 were needed to determine that the best elevation to place the low-distortion projection for the county was not at its average elevation. This is probably not a problem in locations that have little variation in elevation, but in hilly and mountainous regions, the low-distortion projections would need to be severely limited in size to be of any practical use, which then creates the possibility of the need to have multiple projections.
Single Project Factor Using State Plane Coordinates
There is another approach to this problem that is already available on modern survey controllers. That is to use state plane coordinates with a single project scale factor. This project factor is determined as a single combined factor for the project. The requirement for this approach is that the distance distortion be better than those achievable using optical instruments, which in this case I will assume is 1:50,000.
See the next part of this article for a demonstration of the single project factor and Dr. Ghilani’s conclusions on transformations of observations.