Surveying students calculate the Earth’s circumference by following Eratosthene’s method, with help from modern sources.
Surveying and civil engineering technology students (left to right: Wyatt Spencer, Brandon Davis, Jeremy Brunell, B.J. Klenke, Jake Blue, and Joe Irey) plumb up the rod before taking a measurement of the shadow in order to recreate Eratosthenes’ method for calculating the circumference of the Earth.
As part of the Geodetic and Control Surveys class at Dunwoody College of Technology in Minneapolis, Minnesota, we have been studying the history of Eratosthenes and how he calculated the circumference of the Earth. As a class we decided to recreate his method from 276 BC using a similar process.
We thought this would be an interesting way to better understand the methods used back then, and we were curious to see if it would be possible to reenact this process. This knowledge would also help us as we learn about modern datums and methods to approximate the size of the Earth.
Eratosthenes
Eratosthenes’ method for determining the Earth’s circumference.
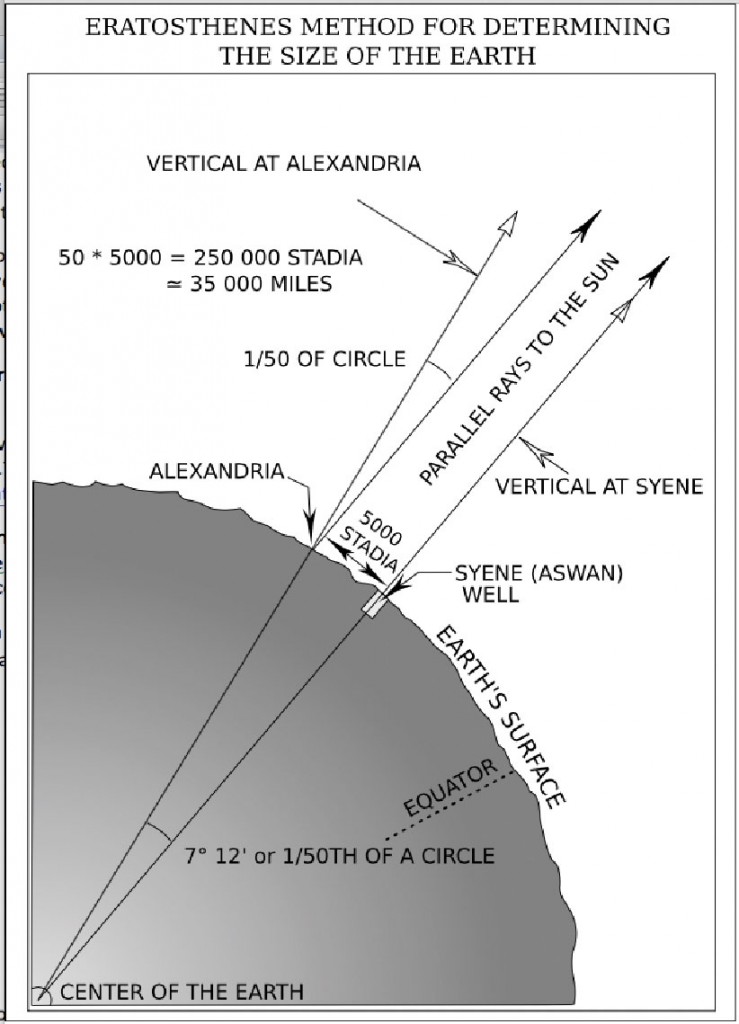
The Greek astronomer Eratosthenes was the first person to compute an accurate measurement of the Earth’s circumference. His process was based on the following elements.
He noted that while looking down a particular well in the city of Syene, Egypt, he could observe that the sun’s reflection was directly in the middle of the water. Thus, he determined on the summer solstice each year that the sun was directly overhead there.
He lived in northern Egypt, in the city of Alexandria, which was 5000 stadia (equal to 500 statute miles) from Syene. On the summer solstice there, he measured the length of the shadow created by a tower. Using simple geometry he calculated the angle between the tower and the shadow and determined the angle to be approximately 7.2°, which is 1/50th of a circle. He then had the distance between Alexandria and Syene measured by averaging the time it took camels to travel between the two cities.
From these observations, Eratosthenes concluded that, since the angular deviation of the sun from the vertical at Alexandria was also the angle of the subtended arc, the linear distance between Alexandria and Syene was 1/50 of the circumference of the Earth or 50 x 500 = 25,000 miles.
His result was remarkably accurate, differing from a value commonly accepted today (24,901 miles at the equator) by less than 100 miles.
Our Reenactment
Our class reenacted this event in a way that was possible for our location on Earth (at Minneapolis), with the sun not directly overhead. We decided to reach out to the forum surveyorconnect.com, as we needed another volunteer to assist us in measuring the angle of the sun’s rays. Dan Robinson of Little
Rock, Arkansas responded to our post and helped us out.
Our data for determining the Earth’s circumference.
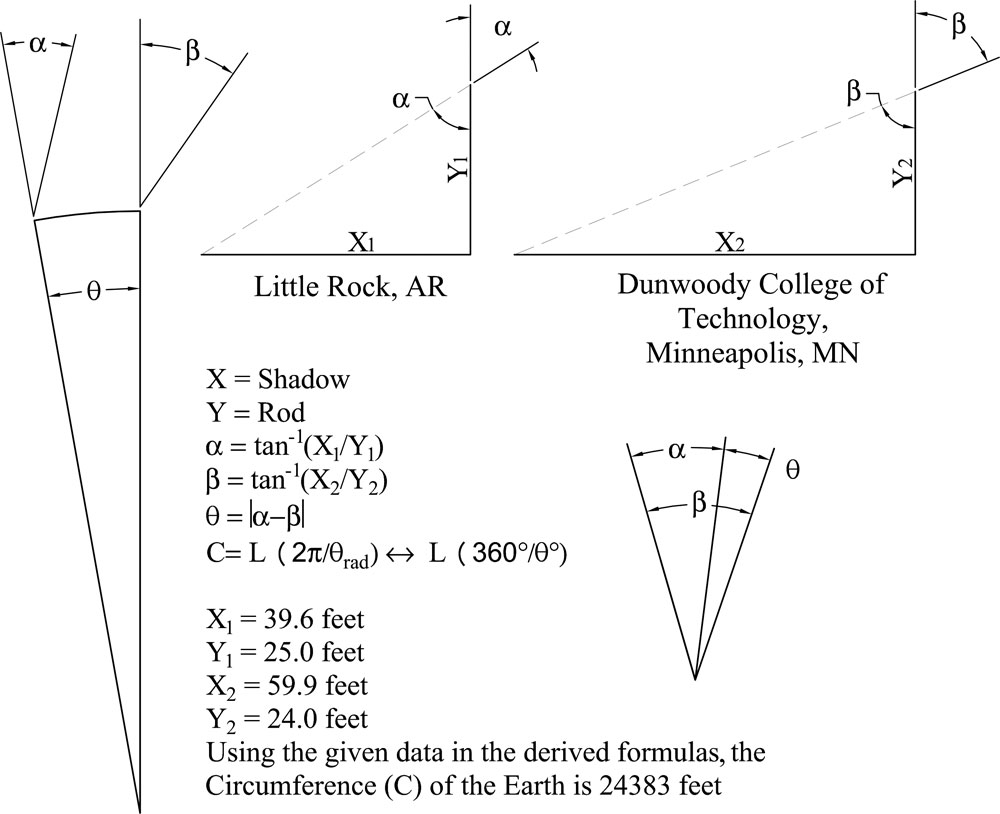
We went out to the front of our school at approximately solar noon. We connected six four-foot range poles to make a 24-foot pole. Then we held the pole vertical and used a plumb bob to confirm that it was vertical. Next, we used a 100-foot tape measure to determine the length of the shadow cast by the range pole. We measured the shadow at 59.9 feet from the base of the pole to the tip of the shadow.
At approximately the same time, solar noon, in Little Rock, Dan measured a shadow of 39.6 feet from a 25-foot pole.
We used the coordinates that Dan gave us for his location (N 44-35-00 W 93-10-00), the coordinates of Dunwoody College (N44-58-22 W93-17-28), and a program to convert coordinates to geodetic distance (movable-type.co.uk/scripts/latlong.html).
Using this process and the formulas shown above, we determined the distance between Dan’s location and ours to be 706.49 miles. We were then able to calculate a circumference of 24,383 miles, which was surprisingly close to the accepted value of 24,901 miles.
We learned that even though modern equipment is capable of locating your position on the Earth with amazing accuracy, it is possible to measure your position with relatively crude equipment, as well.